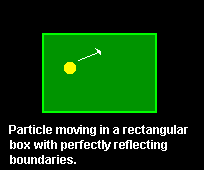
 Consider the idealized case of a particle
restrained to move in a rectangular area.
Assume that the boundaries of the box are perfectly reflecting and that there are no forces acting on the particle.
The motion of the particle is described by the time-dependent Schrödinger equation supplemented with the boundary condition
that the wave function at the edge of the rectangular area is zero. The wave describing the quantum particle is reflected at the boundaries,
a phenomenon analogous to the reflection of light by a mirror.
In general the uncertainty in the position of the particle changes with time.FOOTNOTE 1
The following animations show that as time goes on the probability distribution spreads over the whole box.FOOTNOTE 2
Observe that in the third animation, the probability distribution expands in the direction of propagation only.
Consider the idealized case of a particle
restrained to move in a rectangular area.
Assume that the boundaries of the box are perfectly reflecting and that there are no forces acting on the particle.
The motion of the particle is described by the time-dependent Schrödinger equation supplemented with the boundary condition
that the wave function at the edge of the rectangular area is zero. The wave describing the quantum particle is reflected at the boundaries,
a phenomenon analogous to the reflection of light by a mirror.
In general the uncertainty in the position of the particle changes with time.FOOTNOTE 1
The following animations show that as time goes on the probability distribution spreads over the whole box.FOOTNOTE 2
Observe that in the third animation, the probability distribution expands in the direction of propagation only.
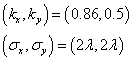

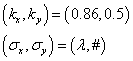
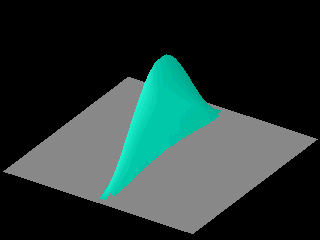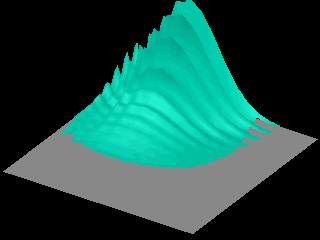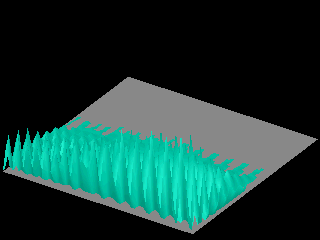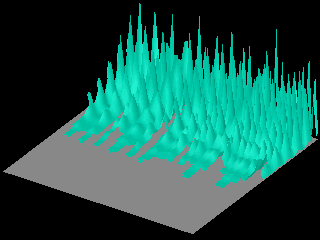
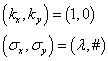
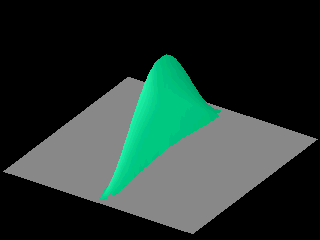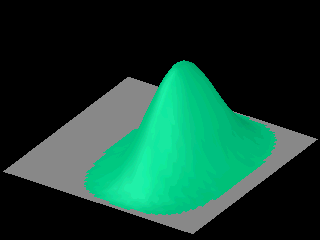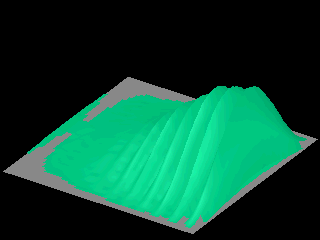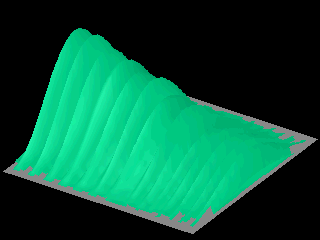
In the third animation the initial wave packet
was chosen such that
Probability distributions that do not change with time, e.g.![]() ,
play an important role in quantum mechanics. If the Hamiltonian does not depend explicitly on time the solution of the time-dependent Schrödinger equation is intimately
related to the solutions of the time-independent Schrödinger equation
,
play an important role in quantum mechanics. If the Hamiltonian does not depend explicitly on time the solution of the time-dependent Schrödinger equation is intimately
related to the solutions of the time-independent Schrödinger equation
Looking for solutions of the time-dependent Schrödinger equation of the form
requires
![]() and
and
![]() to be a solution of the time-independent Schrödinger equation
to be a solution of the time-independent Schrödinger equation
Such solutions represent stationary states of the particle.
Imagine a quantum particle initially described by a Gaussian wave packet centered at the middle of a square box, with momentum zero. As time goes on will the wave packet
- do nothing?
- expand, and contract after being reflected?
- form complex patterns?
Answer (Keep in mind that in the absence of forces a classical particle with zero momentum does not move at all.)
FOOTNOTE 1:
- In the absence of potentials, e.g. if there are no forces acting on the particle, the momentum is a conserved quantity. Therefore the uncertainty in the momentum is also constant.
- From Heisenberg 's uncertainty principle it does NOT follow that an increase in the uncertainty of the position leads to a decrease of the uncertainty in the momentum.
FOOTNOTE 2:
The initial wave function was chosen to be
for the first animation and
for the other two animations. Here
and
![]() is a constant that is fixed by the requirement
that the total probability be normalized to one.
is a constant that is fixed by the requirement
that the total probability be normalized to one.