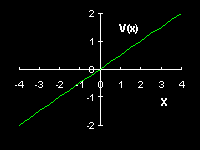
 The potential energy of a charged particle in an electric field along the
The potential energy of a charged particle in an electric field along the
![]() -direction is given by
-direction is given by
![]() ,
where
,
where ![]() denotes the charge of the particle and
denotes the charge of the particle and
![]() sets the strength of the electric field.
The force in the
sets the strength of the electric field.
The force in the ![]() -direction experienced by the particle is
-direction experienced by the particle is
![]() . From Newton's equation of motion
. From Newton's equation of motion
it follows that a classical particle will accelerate in the ![]() -direction only,
up to the point where the particle hits the boundary of the system.
For simplicity it will be assumed that this collision is perfectly elastic.
-direction only,
up to the point where the particle hits the boundary of the system.
For simplicity it will be assumed that this collision is perfectly elastic.
 In two dimensions the motion of a classical particle experiencing the force
In two dimensions the motion of a classical particle experiencing the force
![]() is identical to that of an ideal billiard ball
placed on an ideal billiard table that is tilted in the
is identical to that of an ideal billiard ball
placed on an ideal billiard table that is tilted in the ![]() -direction only.
The following animation shows that the motion in the
-direction only.
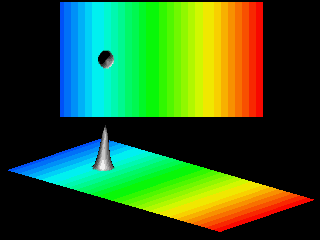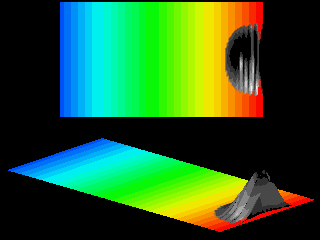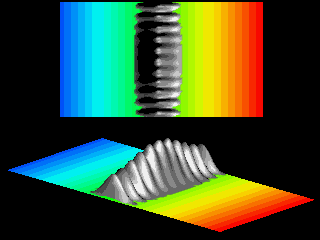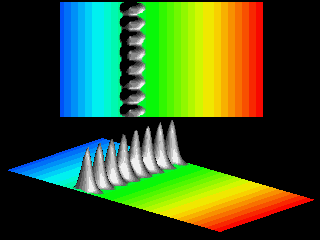
The following animation shows that the motion in the ![]() -direction of a quantum particle on a tilted billiard resembles that of the classical particle:
The wave packet is accelerated and bounces back and forth. In the
-direction of a quantum particle on a tilted billiard resembles that of the classical particle:
The wave packet is accelerated and bounces back and forth. In the
![]() -direction the wave packet is that of a free particle in a box.
-direction the wave packet is that of a free particle in a box.
The acceleration deforms the wave packet, as clearly illustrated in the next movie.

As the velocity in the ![]() -direction increases the wave packet looses its symmetric shape.
The ratio of the spread of the wave packet in
-direction increases the wave packet looses its symmetric shape.
The ratio of the spread of the wave packet in ![]() -
and
-
and ![]() -direction increases.
-direction increases.