 The harmonic oscillator is one of the most important examples in classical and quantum mechanics.
In one dimension harmonic oscillations occur when a particle experiences a restoring force proportional to the displacement from a fixed position.
The concept of harmonic oscillators has proven to be useful to describe the motion of for instance pendulums, vibrating strings,
individual atoms in molecules and in crystals
The harmonic oscillator is one of the most important examples in classical and quantum mechanics.
In one dimension harmonic oscillations occur when a particle experiences a restoring force proportional to the displacement from a fixed position.
The concept of harmonic oscillators has proven to be useful to describe the motion of for instance pendulums, vibrating strings,
individual atoms in molecules and in crystals 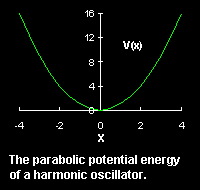 and, on a more abstract level,
the electro-magnetic field.
Whenever the forces between particles are linear functions of the relative displacements the motion of the particles can always be analyzed in terms of harmonic oscillators.
Consider a particle of mass
and, on a more abstract level,
the electro-magnetic field.
Whenever the forces between particles are linear functions of the relative displacements the motion of the particles can always be analyzed in terms of harmonic oscillators.
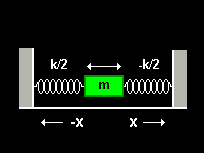
Consider a particle of mass ![]() oscillating in one dimension.
The restoring force acting on the particle is
oscillating in one dimension.
The restoring force acting on the particle is
![]() , where
, where
![]() is called the force or spring constant.
This force derives from the potential energy
is called the force or spring constant.
This force derives from the potential energy
![]() through
through
![]() .
Examples of the motion of a quantum particle in a two-dimensional harmonic potential are shown below.
Note that in one of the movies the wave packet changes with time in one direction only.
The wave function for the other direction was chosen to be a stationary state.
.
Examples of the motion of a quantum particle in a two-dimensional harmonic potential are shown below.
Note that in one of the movies the wave packet changes with time in one direction only.
The wave function for the other direction was chosen to be a stationary state.
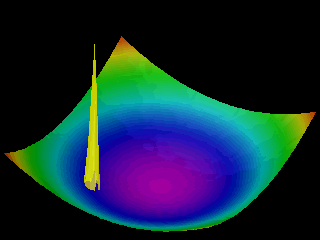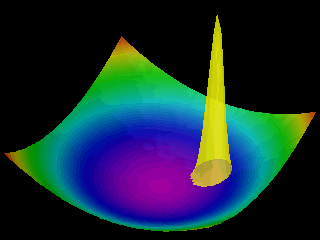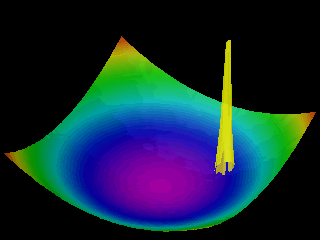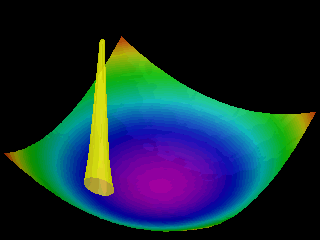
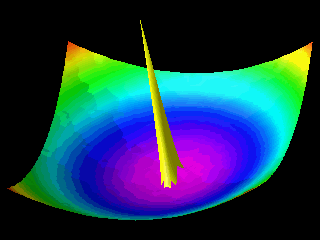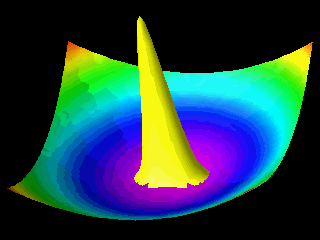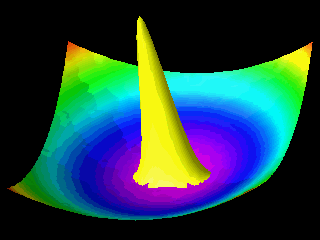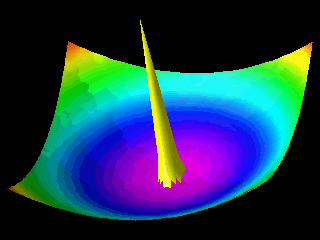
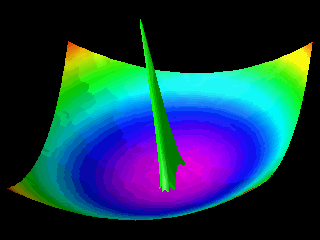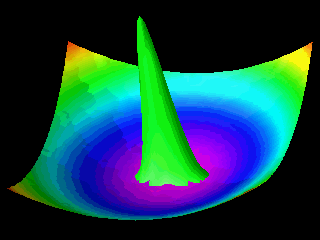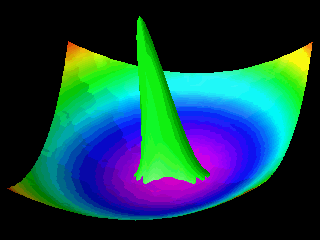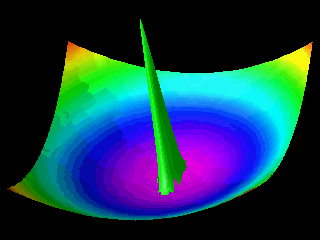
In the first animation the motion of the quantum particle is similar to that of a classical particle. The particle oscillates in the harmonic potential. Meanwhile the wave packet expands and contracts periodically. In the second and third animation the particle has zero momentum. The periodic expansion and contraction of the probability distribution reflects the fact that the particle is not in a stationary state of the harmonic oscillator system.