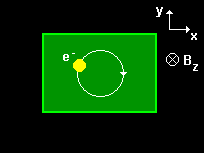
 Classically,
a charged particle in a time-independent homogeneous magnetic field executes a circular motion in the plane perpendicular to the direction of the field.
The period of this motion is the inverse of the cyclotron frequency
Classically,
a charged particle in a time-independent homogeneous magnetic field executes a circular motion in the plane perpendicular to the direction of the field.
The period of this motion is the inverse of the cyclotron frequency
![]() ,
where
,
where
![]() is the strength of the field.
A charged quantum particle in a time-independent homogeneous magnetic field also executes this circular motion.
In addition the probability distribution oscillates harmonically with time.
is the strength of the field.
A charged quantum particle in a time-independent homogeneous magnetic field also executes this circular motion.
In addition the probability distribution oscillates harmonically with time.

In the coordinate system attached to the moving center of the wave packet, the particle experiences a harmonic potential leading to the harmonic, time-dependent distortion of the wave packet. The next picture shows a sequence of snapshots illustrating the oscillation of the wave packet.

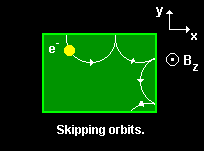 If the circular motion of a classical charged particle in the plane perpendicular to the direction of a uniform magnetic field is interrupted by reflection from a boundary,
the particle executes so-called skipping orbits. Try to imagine what happens to the quantum particle.
If the circular motion of a classical charged particle in the plane perpendicular to the direction of a uniform magnetic field is interrupted by reflection from a boundary,
the particle executes so-called skipping orbits. Try to imagine what happens to the quantum particle.

The charged quantum particle follows the skipping orbits of the classical particle as long as the whole wave packet is reflected by a single boundary. Once the wave packet has entered a corner it becomes difficult to identify the skipping orbits.