The time evolution of a quantum system follows from the solution of the TDSE, the Time-Dependent Schrödinger Equation.
For simplicity consider the TDSE describing a system that can be in no more than two states. For a quantum system that has only two possible states
![]() and
and
![]() the TDSE reads
the TDSE reads
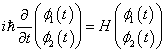
where
is the Hamiltonian describing the system.
The solution of this equation gives a complete description of the time evolution of the quantum system.
For instance, the probability to find the system in state 1 at time
![]() is given by
is given by
The Hamiltonian for a particle in an electromagnetic potential is given by

The quantum state of the particle is characterized by the amplitude
![]() for any point in space and time.
This amplitude is also called the wave function of the particle.
As before, the TDSE governs the time evolution of the wave function.
The probability to find the particle at the position
for any point in space and time.
This amplitude is also called the wave function of the particle.
As before, the TDSE governs the time evolution of the wave function.
The probability to find the particle at the position
![]() at time
at time
![]() is given by
is given by
The wave function contains all the information about the quantum system. Once it is known for all points in space and time, any physical quantity can be calculated.