The theory of quantum mechanics asserts that with every possibility for an event in nature to take place, there is a quantity called amplitude associated with each alternative.
Furthermore, the amplitude associated with the overall event is obtained by adding the amplitudes of each of the alternatives.
The probability that the event will happen is equal to the square of the absolute value of the overall amplitude.
Thus, if
![]() and
and
![]() are the amplitudes of the two possibilities for a particular event to take place,
the amplitude for the total event is
are the amplitudes of the two possibilities for a particular event to take place,
the amplitude for the total event is
and the probability for the event to occur is given by
In the macroscopic world the total probability for an event to take place is given by
the sum of the probabilities of each alternative. In quantum mechanics
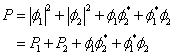
The two additional terms are due to the interference of alternatives. If the event is interrupted before its conclusion, for example by determining if the event takes place through alternative 1, the amplitudes of all other alternatives can no longer be added to the total amplitude.