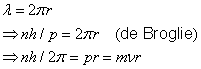Particle / wave character of the electron
de Broglie postulated, based on relativistic considerations, that particles should be assigned a wavelength (the de Broglie wavelength)
where ![]() is the momentum of the particle and
is the momentum of the particle and
![]() is Planck´s constant.
For the wave associated with a particle moving in the
is Planck´s constant.
For the wave associated with a particle moving in the
![]() -direction, de Broglie proposed the harmonic wave function
-direction, de Broglie proposed the harmonic wave function
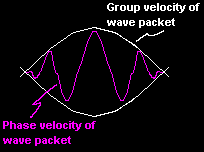 The physically important result of his ideas is that there are two velocities associated with the waves.
One is the phase velocity (
The physically important result of his ideas is that there are two velocities associated with the waves.
One is the phase velocity ( ![]() ) and the second is a
group velocity
) and the second is a
group velocity ![]() which coincides with the velocity of the particle.
which coincides with the velocity of the particle.
de Broglie suggested that the wave properties of particles could be confirmed experimentally by the observation of diffraction effects when electrons are incident on crystals. Experimental evidence for the wave nature of electrons was found by Davisson and Germer, who observed the scattering of a beam of electrons from a nickel crystal. At about the same time, G.P. Thomson (the son of J.J. Thomson) succeeded in demonstrating electron diffraction in scattering experiments with thin films of metals. Now there is a theoretical justification for the orbital quantization (Bohr´s first postulate). When the electron moves around in an atom, its associated wave is stationary, i.e. in a standing wave pattern for which
Hence