Optical line spectra
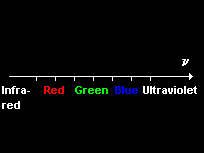 Each element emits and absorbs its own characteristic line spectrum consisting of a unique set of discrete frequencies.
The lines can be grouped into series in which lines become more closely spaced with decreasing wavelength, approaching a series limit at which the line spacing converges to zero.
Each element emits and absorbs its own characteristic line spectrum consisting of a unique set of discrete frequencies.
The lines can be grouped into series in which lines become more closely spaced with decreasing wavelength, approaching a series limit at which the line spacing converges to zero.
Does an equation exist that gives the wavelengths of any series?
In 1885 J.J. Balmer constructed a formula which predicted almost exactly the frequencies of the four visible hydrogen lines, measured accurately in 1862 by Angstrom
The general formula was developed by Rydberg in 1890
where
![]() is called the Rydberg constant. For the Balmer series
is called the Rydberg constant. For the Balmer series
![]() .
Other series are the Lyman series (
.
Other series are the Lyman series (![]() , ultraviolet, 1906-1914),
the Paschen series (
, ultraviolet, 1906-1914),
the Paschen series (![]() , infrared, 1908) and the Brackett series
(
, infrared, 1908) and the Brackett series
(![]() , infrared, 1922).
The sequences strongly suggested some kind of energy diagram as the emission / absorption of light from an atom must correspond to a decrease / increase in the atom's energy.
This information would be critical to any atomic theory.
, infrared, 1922).
The sequences strongly suggested some kind of energy diagram as the emission / absorption of light from an atom must correspond to a decrease / increase in the atom's energy.
This information would be critical to any atomic theory.
 In 1897 J.J. Thomson discovered the electron. He demonstrated that the electron had a distinct charge-to-mass ratio and was thus a particle, not a cathode ray.
Thomson and Lord Kelvin developed a model of the atom in which the negative electrons were embedded in a uniform sphere of positive charge.
They assumed that the radiation should be described by Maxwell's electromagnetic theory and that the dynamics in the atom should obey Newton´s law of motion.
The model was inherently unstable, i.e. no configuration of the charges can be in stable equilibrium. In 1908 Rutherford performed experiments on alpha-scattering by a thin gold foil.
He concluded that an atom contains a positive nucleus possessing almost all of the atom's mass in a tiny fraction of its volume.
This poses some questions. What is the arrangement of the electrons? Why does the electron not fall in the nucleus?
In 1897 J.J. Thomson discovered the electron. He demonstrated that the electron had a distinct charge-to-mass ratio and was thus a particle, not a cathode ray.
Thomson and Lord Kelvin developed a model of the atom in which the negative electrons were embedded in a uniform sphere of positive charge.
They assumed that the radiation should be described by Maxwell's electromagnetic theory and that the dynamics in the atom should obey Newton´s law of motion.
The model was inherently unstable, i.e. no configuration of the charges can be in stable equilibrium. In 1908 Rutherford performed experiments on alpha-scattering by a thin gold foil.
He concluded that an atom contains a positive nucleus possessing almost all of the atom's mass in a tiny fraction of its volume.
This poses some questions. What is the arrangement of the electrons? Why does the electron not fall in the nucleus?
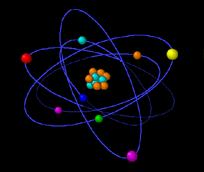 Rutherford proposed a planetary model for the atom. BUT if the electrons are like a microscopic solar system,
moving in circular orbits about the nucleus (and thus accelerating) what keeps the electrons from radiating continuously as the classical electromagnetic theory would predict?
Rutherford´s model was unstable.
Rutherford proposed a planetary model for the atom. BUT if the electrons are like a microscopic solar system,
moving in circular orbits about the nucleus (and thus accelerating) what keeps the electrons from radiating continuously as the classical electromagnetic theory would predict?
Rutherford´s model was unstable.
Around 1912 Bohr postulated:
- The only allowed orbits for the electrons are characterized by values of orbital angular momentum given by
These orbits are called stationary states.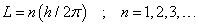
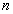 is called the principle quantum number.
From the angular momentum of the orbiting electron Bohr calculated the radius and the energy of the orbits using classical ideas. The angular momentum is
is called the principle quantum number.
From the angular momentum of the orbiting electron Bohr calculated the radius and the energy of the orbits using classical ideas. The angular momentum is
where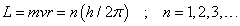
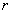 is the orbit radius,
is the orbit radius,
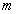 is the mass of the electron and
is the mass of the electron and
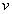 is the velocity of the electron.
Another equation comes from setting the Coulomb force on the electron equal to the product of its mass and its centripetal acceleration
is the velocity of the electron.
Another equation comes from setting the Coulomb force on the electron equal to the product of its mass and its centripetal acceleration
where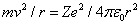
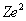 is the product of the nuclear charge
is the product of the nuclear charge
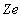 and the electron charge
and the electron charge
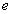 ,
,
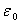 is the dielectric constant of vacuum. Hence it follows that
is the dielectric constant of vacuum. Hence it follows that
The smallest radius is for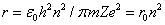
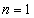 . For hydrogen (
. For hydrogen (
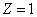 ) its value is
) its value is
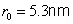 .
At this value, called the Bohr radius, the hydrogen atom is in its ground state (i.e. its energy is in a minimum). The energy of the stationary states is given by
.
At this value, called the Bohr radius, the hydrogen atom is in its ground state (i.e. its energy is in a minimum). The energy of the stationary states is given by
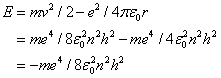
- A transition of the electron between two stationary states will produce an emission or absorption of radiation, with a frequency given by the Planck / Einstein relation
where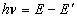
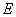 and
and
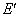 are the energies of the atom in the initial and final stationary states.
are the energies of the atom in the initial and final stationary states.
From these postulates Bohr derived Balmer´s formula
Bohr calculated Rydberg's constant
![]() converting
converting
![]() from an empirical constant to a derived quantity.
Note that the above equations cannot be generalized to systems with more than one electron.
from an empirical constant to a derived quantity.
Note that the above equations cannot be generalized to systems with more than one electron.
As more accurate measurements of the hydrogen spectra came available, lines seen previously as single lines seemed to be closely spaced multiple lines
(i.e. the fine structure in atomic spectra). Moreover the Bohr theory predicted too many spectrum lines.
Hence Bohr´s atom model with only one quantum number was too simple.
Sommerfeld modified the Bohr model by introducing elliptical orbits, using a second quantum number
![]() , also quantized in units of
, also quantized in units of
![]() .
The number
.
The number ![]() still gives the energy, but
the number
still gives the energy, but
the number ![]() ,
which can be any integer less than or equal to
,
which can be any integer less than or equal to ![]() , gives the angular momentum.
, gives the angular momentum.
When excited atoms are placed in a magnetic field extraneous spectral lines appear, as shown by P. Zeeman in 1896.
This effect, now known as the Zeeman effect, could not be explained by the Bohr-Sommerfeld atomic model on the basis of the two quantum numbers
![]() and
and
![]() .
Sommerfeld introduced a third quantum number, the magnetic quantum number
.
Sommerfeld introduced a third quantum number, the magnetic quantum number
![]() .
The orientation of the orbit with respect to the magnetic field should also be quantized.
.
The orientation of the orbit with respect to the magnetic field should also be quantized.
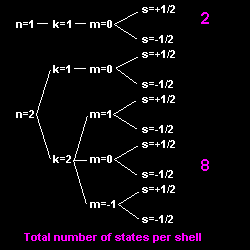 The Bohr-Sommerfeld model
based on the three quantum numbers
The Bohr-Sommerfeld model
based on the three quantum numbers ![]() ,
,
![]() ,
,
![]() could explain the Zeeman effect.
But later magnetic experiments producing again more lines could not be explained. This effect was called the anomalous Zeeman effect.
The anomalous Zeeman effect is a consequence of electron´s spinning.
W. Pauli proposed a fourth quantum number
could explain the Zeeman effect.
But later magnetic experiments producing again more lines could not be explained. This effect was called the anomalous Zeeman effect.
The anomalous Zeeman effect is a consequence of electron´s spinning.
W. Pauli proposed a fourth quantum number
![]() having values ± 1/2.
Note that the angular momentum of the spinning electron is one-half of the normal value
having values ± 1/2.
Note that the angular momentum of the spinning electron is one-half of the normal value
![]() of atomic orbits, so-called spin 1/2.
of atomic orbits, so-called spin 1/2.
To explain why in the atomic structure all the electrons do not simply fall into the state of lowest energy (i.e. the "ground" state), Pauli proposed the exclusion principle (1925): No more than one electron can be in any given orbital and spin state. This gives each element its characteristic structure. The periodic table of the elements (1890, D. Mendeléev) could now be understood from first principles. However, note that Bohr already explained the periodicity of the elements, using his orbital model, before Pauli's discovery. The exclusion principle generates the magic numbers, i.e. how many electrons are in each orbit or shell.