The following animation shows the diffraction of a Gaussian wave packet by two slits. In this case there is no magnetic field.
The angular distribution
recorded by a detector placed far away from a source characterizes the interference pattern.
For zero magnetic field
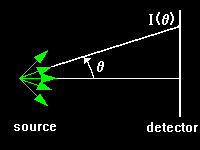the simulation yields an angular distribution
that is in excellent agreement with the Fraunhofer diffraction pattern of a double slit.
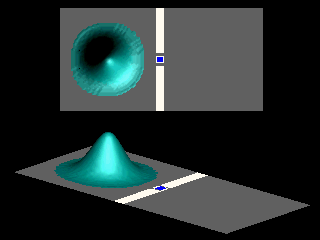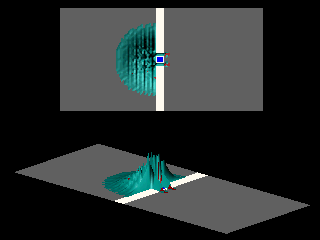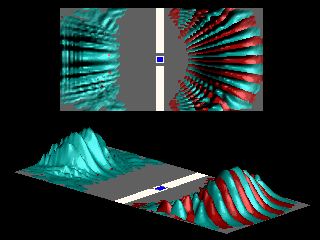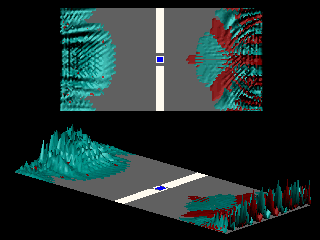
The next animation illustrates the Aharonov-Bohm effect. The magnetic field is confined to the red area and is chosen such that the shift in the interference pattern is as large as possible.
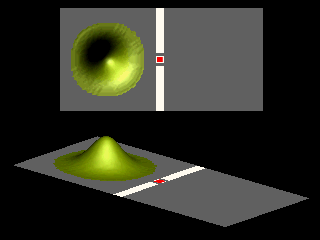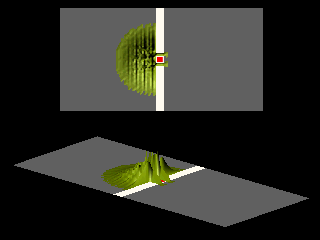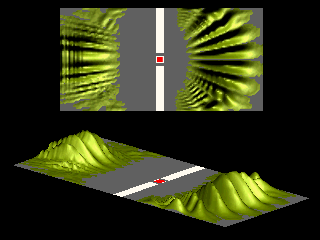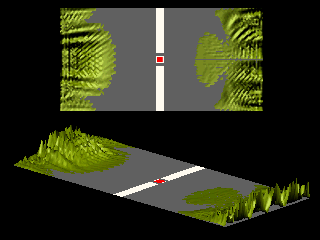
Inspection of the angular distribution shows that compared to the zero field case the maxima and the minima are interchanged:
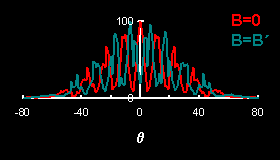
The diffraction pattern is shifted by an angle
.
In general,
, where
is the magic field for which
.
The interchange of maxima and minima can also be demonstrated by superimposing the animations for zero and magic magnetic field.
In the animation that follows only the blue colored wave packet is affected by the vector potential.
