The necessary conditions to observe the Aharonov-Bohm effect, i.e. a shift of the diffraction pattern that varies periodically with
![]() , are:
, are:
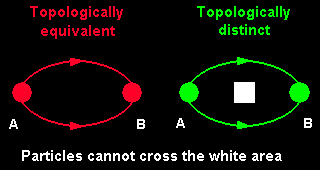
- There must be at least two interfering alternatives for the particle to arrive at the detector, and
- At least two of these interfering alternatives must enclose a shielded magnetic field and must be topologically distinct.
The next two animations illustrate the importance of the first condition.
Each animation shows the superposition of the waves for the case with (in blue) and without (in red) a magnetic field.
The field
![]() .
.

The Aharonov-Bohm effect vanishes as the number of interfering alternatives decreases. As illustrated in the following animation, increasing the width of and the distance between the two slits reduces the amount of scattering and therefore also the Aharonov-Bohm effect.
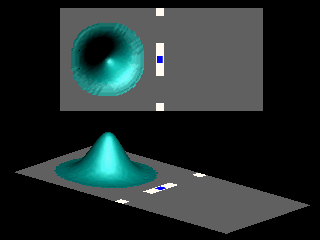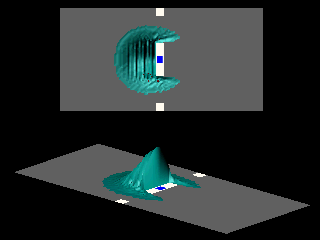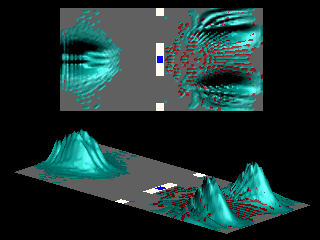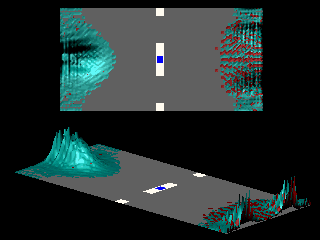
Turning the double slit into a single slit changes the topology of the space accessible to the particle. In the absence of a magnetic field the interference pattern is that of a single slit.

When the magnetic field inside the slit is turned on the particle experiences the Lorentz force, resulting in a displacement of the diffraction pattern as a whole. However, this displacement is not a periodic function of the applied field.
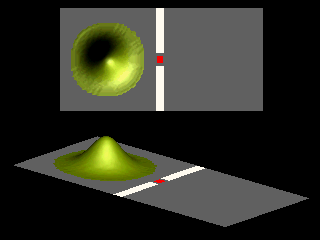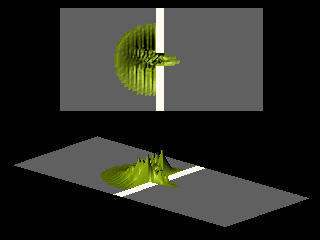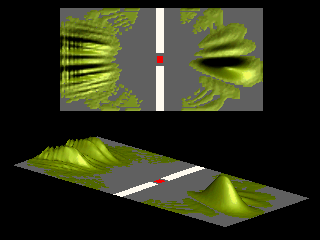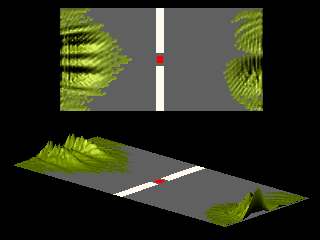
Inspection of the angular distribution shows that compared to the zero field case the maximum is shifted:
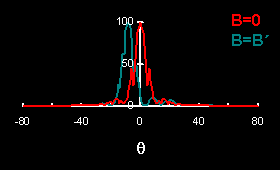
In this simply-connected geometry there is no systematic interchange of the maxima and minima of the diffraction pattern.
The following animation shows the superposition of the
![]() (in red) and
(in red) and
![]() (in blue) simulations.
(in blue) simulations.

For a single-slit geometry the Aharonov-Bohm effect is suppressed because there are no topologically distinct paths for the particle to pass through the slit.