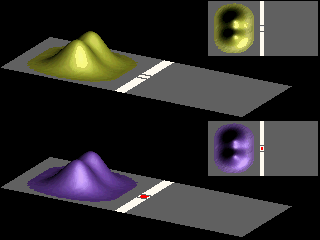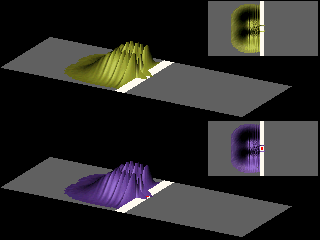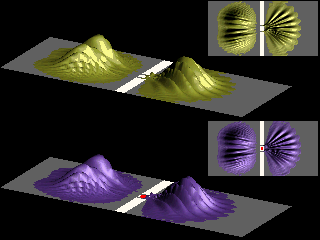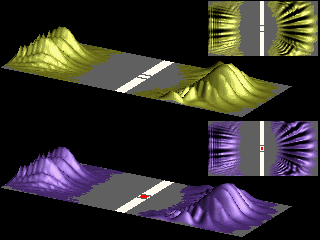
Two identical fermions, e.g. two electrons with the same spin orientation, cannot occupy the same point in space, nor can they have the same value of momentum.
 Identical fermions must obey this exclusion principle. The picture on the right
shows a probability distribution of two identical fermions.
The dip between the two maxima reflects the fact that the two fermions cannot occupy the same point in space.
The animations show the time development of the probability distribution of the two fermions, for the case that there is no interaction potential between the fermions.
Upper part: Double-slit (in white), no magnetic field. Lower part: Double-slit (in white), confined magnetic field (in red).
Identical fermions must obey this exclusion principle. The picture on the right
shows a probability distribution of two identical fermions.
The dip between the two maxima reflects the fact that the two fermions cannot occupy the same point in space.
The animations show the time development of the probability distribution of the two fermions, for the case that there is no interaction potential between the fermions.
Upper part: Double-slit (in white), no magnetic field. Lower part: Double-slit (in white), confined magnetic field (in red).
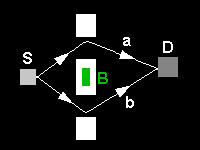 The magnetic flux through the red area is chosen such that for a single particle the shift in the diffraction pattern due to the Aharonov-Bohm effect is 180°.
The magnetic flux through the red area is chosen such that for a single particle the shift in the diffraction pattern due to the Aharonov-Bohm effect is 180°.
The animation shows the interchange of the maxima and minima of the probability distribution, due to the Aharonov-Bohm effect.
The salient features of the intensity measured by detector ![]() are the same as for the case where the source
are the same as for the case where the source
![]() emits a single particle.
emits a single particle.
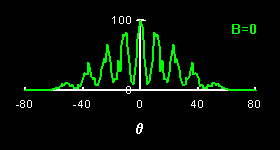
The fermionic nature of the wave reveals itself in the cross-correlated signal
![]() of the detectors
of the detectors
![]() and
and
![]() .
.
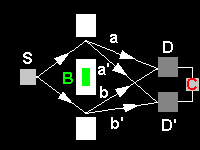 Just as for a detector measuring the angular distribution, the positions of the detectors are specified by the angles
Just as for a detector measuring the angular distribution, the positions of the detectors are specified by the angles
![]() and
and
![]() .
.
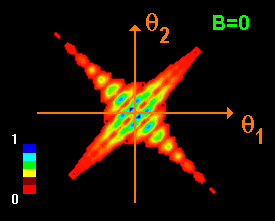

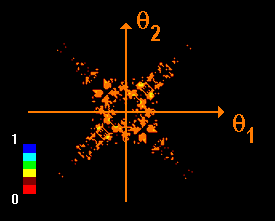
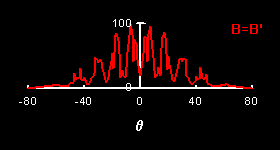
The correlated two-particle signal also shows the Aharonov-Bohm effect, as can be clearly seen by substracting the
![]() and
and
![]() signals.
signals.